DWAINE Telescience: Difference between revisions
m →Formula |
m →Relay |
||
| (4 intermediate revisions by the same user not shown) | |||
| Line 58: | Line 58: | ||
The relay command attempts to receive from a coordinate '''X1 Y1 Z1''' and send to a coordinate '''X2 Y2 Z2'''. It operates as if the user first sends the receive command then the send command. | The relay command attempts to receive from a coordinate '''X1 Y1 Z1''' and send to a coordinate '''X2 Y2 Z2'''. It operates as if the user first sends the receive command then the send command. | ||
<code>teleman -p 1 X1 Y1 Z1 X2 Y2 Z2</code> | <code>teleman -p 1 relay X1 Y1 Z1 X2 Y2 Z2</code> | ||
== Finding valid coordinates == | == Finding valid coordinates == | ||
| Line 93: | Line 93: | ||
===== Slope ===== | ===== Slope ===== | ||
Lets take <code>Real Coordinate = Slope * | Lets take <code>Real Coordinate = Slope * Tmaxc - Intercept</code> and get the highest value the Real Coordinate can go, that is 300, with <code>Tmaxc</code> being the highest valid terminal coordinate we can go. | ||
<code>300 = Slope * | <code>300 = Slope * Tmaxc - Intercept</code> | ||
If we then rearrange to find the intercept: | If we then rearrange to find the intercept: | ||
<code>Intercept = Slope * | <code>Intercept = Slope * Tmaxc - 300</code> | ||
Now we need to find a value for the intercept that satisfies the equation <code>100 >= Intercept >= 0</code>. That means <code>100 >= Slope * | Now we need to find a value for the intercept that satisfies the equation <code>100 >= Intercept >= 0</code>. That means <code>100 >= Slope * Tmaxc - 300 >= 0</code>, <code>400 >= Slope * Tmaxc >= 300</code> | ||
* <code>Slope = 1</code>: <code>400 >= | * <code>Slope = 1</code>: <code>400 >= Tmaxc >= 300</code> | ||
* <code>Slope = 2</code>: <code>200 >= | * <code>Slope = 2</code>: <code>200 >= Tmaxc>= 150</code> | ||
* <code>Slope = 4</code>: <code>100 >= | * <code>Slope = 4</code>: <code>100 >= Tmaxc>= 75</code> | ||
Meaning: If we scan 300 and its a valid coordinate, it means the slope is 1 otherwise its either 2 or 4. Doing the test again for 150 will give the slope of the equation. | Meaning: If we scan 300 and its a valid coordinate, it means the slope is 1 otherwise its either 2 or 4. Doing the test again for 150 will give the slope of the equation. | ||
| Line 110: | Line 110: | ||
===== Intercept ===== | ===== Intercept ===== | ||
Given that we now know the slope, we can test values to find the highest <code>Tc</code> we can find, which we will call <code> | Given that we now know the slope, we can test values to find the highest <code>Tc</code> we can find, which we will call <code>Tmaxc</code>. | ||
With the maximum value on the real coordinate, we need to find the highest terminal coordinate that does not give an error on the terminal when scanned. | With the maximum value on the real coordinate, we need to find the highest terminal coordinate that does not give an error on the terminal when scanned. | ||
This coordinate <code> | This coordinate <code>Tmaxc</code> will satisfy the equation: <code>Intercept = Slope * Tc - 300</code> | ||
'''Note''' | |||
* <code>Slope = 1</code>: Tc moves in multiples of <code>1/1 = 1</code> | |||
* <code>Slope = 2</code>: Tc moves in multiples of <code>1/2 = 0.5</code> | |||
* <code>Slope = 4</code>: Tc moves in multiples of <code>1/4 = 0.25</code> | |||
{| class="wikitable" | {| class="wikitable" | ||
| Line 131: | Line 136: | ||
| <code>Tc = 159</code> || Invalid || Go lower | | <code>Tc = 159</code> || Invalid || Go lower | ||
|- | |- | ||
| <code>Tc = 158.5</code> || Valid || <code> | | <code>Tc = 158.5</code> || Valid || <code>Tmaxc = 158.5</code>, therefore <code>Intercept = 2 * 158.5 - 300 = 17</code> | ||
|} | |} | ||
==== Formula ==== | ==== Formula ==== | ||
Now that we know the slope and intercept, we can simply further the formula. | |||
<!-- Latex Formula Used | |||
R_{coord} = Slope * T_{coord} - Intercept \newline | |||
R_{coord} = Slope * T_{coord} - (Slope * T_{maxcoord} - 300) \newline | |||
T_{coord} = \frac{Slope * T_{maxcoord} + R_{coord} - 300}{Slope} | |||
--> | |||
[[File:DwaineTelesciTcFormula.png|none|none|alt=Tc = (Slope * Tmaxc + Rc - 300) / Slope|TC Formula]] | |||
In a terminal this could be written as: <code>eval $Slope $Tmaxc * $Rc + 300 - $Slope / to Tc</code> | |||
'''Note: Do not use <code>,</code> for decimals in DWAINE. Use <code>.</code> instead.''' | |||
==== Putting it all together ==== | |||
It's round start and you are a bored AI. Lets try finding the slope and intercept for the X, Y axis and a valid z-level for the Z coordinate. | |||
It is less confusing to do one axis at a time, but more experienced players will do both at once to save time. | |||
{| class="wikitable" | |||
|+ Caption Coordinates | |||
|- | |||
! X !! Y !! Z !! Teleman !! | |||
|- | |||
| '''300''' || 300 || 1 || <code>]Invalid coordinates (YZ)</code> || <code>SlopeX = 1</code> | |||
|- | |||
| 350 || 150 || 2 || <code>]Invalid coordinates (YZ)</code> || If <code>Tcy = 150</code> is invalid, then we know that <code>SlopeY = 4</code> so <code>Tcy = 75</code> will be valid. | |||
|- | |||
| 375 || 85 || 3 || <code>]Invalid coordinates (XZ)</code> || | |||
|- | |||
| 365 || 95 || 4 || <code>]No atmosphere.</code> || The station z-level is the first available, so <code>Station Z-Level = 4</code>. | |||
|- | |||
| 368 || 98 || 4 || <code>]Invalid coordinates (X)</code> || | |||
|- | |||
| '''367''' || 99 || 4 || <code>]Invalid coordinates (Y)</code> || <code>Tmaxcx = 367</code> | |||
|- | |||
| 367 || 98.75 || 4 || <code>]Invalid coordinates (Y)</code> || | |||
|- | |||
| 367 || 98.50 || 4 || <code>]Invalid coordinates (Y)</code> || | |||
|- | |||
| 367 || '''98.25''' || 4 || <code>]No atmosphere.</code> || <code>Tmaxcy = 98.25</code> | |||
|} | |||
From this info we can gather: | |||
{| class="wikitable" | |||
|- | |||
! !! Slope !! Max Coordinate !! Intercept | |||
|- | |||
| '''X''' || 1 || 367 || 67 | |||
|- | |||
| '''Y''' || 4 || 98.25 || 93 | |||
|} | |||
== Griefing == | |||
Since anyone who can fake a SU access to Dwaine can access teleman, it means anyone can interfere with TeleScience work. | |||
Setting the telepad coordinates remotely will not update in the telescience computer, which in turns makes scientists very confused when the coordinate in their computer sends them to a very different location or explodes in their face. | |||
In | In case of interference, players will usually always blame the AI first. | ||
Latest revision as of 14:33, 25 April 2023
| This page is under construction. The following information may be incomplete. You can help by adding missing information or formatting. |
Introduction
The DWAINE computer is powerful tool that still surrounded by a lot of mystery. This page aims to teach its user how to operate a Telescience teleport pad.
Scripting
The telesci commands are very repetitive, thus its better if you use scripts to facilitate your job. Either make your own or use existing scripts.
Basic Commands
Access to the teleman requires Super User Access. The program itself is located at /sys/srv/teleman but its easier to work with if its copied to your home directory.
Telepad ID
Every telepad connected to the mainframe has its own ID number which increases sequentially in number starting at 1. The telepad can be referenced by using -p ID. Running teleman without specifying the ID will default to 1.
Setting coordinates
Before using other commands the teleman must be first configured to a coordinate.
teleman -p 1 coords X Y Z sets the teleporter pad coordinates. This process is very repetitive, thus its better
Scanning
After the coordinates are set the telepad is ready to receive commands.
teleman -p 1 scan will scan the coordinate and return to you whether the coordinate you selected leads to an invalid coordinate or not.
Example Outputs
]Invalid coordinates (XYZ): The coordinates inside the parentheses are invalid.]No atmosphere.: The coordinate is valid but it leads to somewhere without atmosphere, likely space.]Atmosphere: O2: 21.8249, N2: 82.1031, CO2: 0, Plasma: 0, Farts: 0, Fallout: 0, 293.15 Kelvin, 101.325 kPa,: Coordinate is valid and leads to somewhere with an atmosphere.
Send
Sends the object or person on the telepad to the configured coordinate.
teleman -p 1 send
Receive
Receives the object or person on configured coordinate to the telepad.
teleman -p 1 receive
Portal
Creates a portal on the telepad linked to the configured coordinate.
teleman -p 1 portal
Relay
A bit different from the other commands, this one doesn't need to have a coordinate configured first.
The relay command attempts to receive from a coordinate X1 Y1 Z1 and send to a coordinate X2 Y2 Z2. It operates as if the user first sends the receive command then the send command.
teleman -p 1 relay X1 Y1 Z1 X2 Y2 Z2
Finding valid coordinates
Space GPS
The section in Telescience - Decoding the teleporter goes in detail on how to get valid coordinates using the space GPS.
Utilizing a website like Vortex1942 Telescience Map is also very helpful.
The 300 300 Method
Sometimes using a space GPS it not an option, either because you're too far away from the telepad or if you're an AI without any cyborg shells with their built in PDA Space GPS. This math heavy section aims to teach a more savy player how to find telescience coordinates using only the teleman command. If you haven't already, you're strongly recommended to get some scripts for this part.
Map Coordinates
The map is a 300 x 300 grid that starts at 1 and ends at 300. Every coordinate outside this range is an invalid coordinate.
Offsets
- Rc: Real coordinate ( map coordinate, the one you can find with the space gps )
- Tc: Terminal coordinate ( coordinate you send to teleman )
The formula for a coordinate is a simple linear function (y = a * x + b):
Real Coordinate = Slope * Tc - Intercept
Each axis X and Y have their own slope and intercept values.
The slope only has one of three values: 1, 2 and 4.
The intercept is a random integer from 0 to 100 inclusive.
Slope
Lets take Real Coordinate = Slope * Tmaxc - Intercept and get the highest value the Real Coordinate can go, that is 300, with Tmaxc being the highest valid terminal coordinate we can go.
300 = Slope * Tmaxc - Intercept
If we then rearrange to find the intercept:
Intercept = Slope * Tmaxc - 300
Now we need to find a value for the intercept that satisfies the equation 100 >= Intercept >= 0. That means 100 >= Slope * Tmaxc - 300 >= 0, 400 >= Slope * Tmaxc >= 300
Slope = 1:400 >= Tmaxc >= 300Slope = 2:200 >= Tmaxc>= 150Slope = 4:100 >= Tmaxc>= 75
Meaning: If we scan 300 and its a valid coordinate, it means the slope is 1 otherwise its either 2 or 4. Doing the test again for 150 will give the slope of the equation.
Intercept
Given that we now know the slope, we can test values to find the highest Tc we can find, which we will call Tmaxc.
With the maximum value on the real coordinate, we need to find the highest terminal coordinate that does not give an error on the terminal when scanned.
This coordinate Tmaxc will satisfy the equation: Intercept = Slope * Tc - 300
Note
Slope = 1: Tc moves in multiples of1/1 = 1Slope = 2: Tc moves in multiples of1/2 = 0.5Slope = 4: Tc moves in multiples of1/4 = 0.25
Tc = 300 |
Invalid | Slope = 2 or Slope = 4
|
Tc = 150 |
Valid | Slope = 2
|
Tc = 170 |
Invalid | Go lower |
Tc = 155 |
Valid | Go higher |
Tc = 158 |
Valid | Go higher |
Tc = 159 |
Invalid | Go lower |
Tc = 158.5 |
Valid | Tmaxc = 158.5, therefore Intercept = 2 * 158.5 - 300 = 17
|
Formula
Now that we know the slope and intercept, we can simply further the formula.
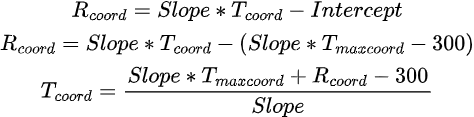
In a terminal this could be written as: eval $Slope $Tmaxc * $Rc + 300 - $Slope / to Tc
Note: Do not use , for decimals in DWAINE. Use . instead.
Putting it all together
It's round start and you are a bored AI. Lets try finding the slope and intercept for the X, Y axis and a valid z-level for the Z coordinate.
It is less confusing to do one axis at a time, but more experienced players will do both at once to save time.
| X | Y | Z | Teleman | |
|---|---|---|---|---|
| 300 | 300 | 1 | ]Invalid coordinates (YZ) |
SlopeX = 1
|
| 350 | 150 | 2 | ]Invalid coordinates (YZ) |
If Tcy = 150 is invalid, then we know that SlopeY = 4 so Tcy = 75 will be valid.
|
| 375 | 85 | 3 | ]Invalid coordinates (XZ) |
|
| 365 | 95 | 4 | ]No atmosphere. |
The station z-level is the first available, so Station Z-Level = 4.
|
| 368 | 98 | 4 | ]Invalid coordinates (X) |
|
| 367 | 99 | 4 | ]Invalid coordinates (Y) |
Tmaxcx = 367
|
| 367 | 98.75 | 4 | ]Invalid coordinates (Y) |
|
| 367 | 98.50 | 4 | ]Invalid coordinates (Y) |
|
| 367 | 98.25 | 4 | ]No atmosphere. |
Tmaxcy = 98.25
|
From this info we can gather:
| Slope | Max Coordinate | Intercept | |
|---|---|---|---|
| X | 1 | 367 | 67 |
| Y | 4 | 98.25 | 93 |
Griefing
Since anyone who can fake a SU access to Dwaine can access teleman, it means anyone can interfere with TeleScience work.
Setting the telepad coordinates remotely will not update in the telescience computer, which in turns makes scientists very confused when the coordinate in their computer sends them to a very different location or explodes in their face.
In case of interference, players will usually always blame the AI first.
